Infos zur linearen Funktion: 

Funktionen, deren Graphen im Koordinatensystem eine Gerade ergeben, nennt man lineare Funktionen. Wie steil der Graph verläuft, ist durch den Steigungsfaktor m festgelegt.
 Funktionsgleichung   Steigungsfaktor   Verschiebungskonstante 
 y =  m  • x +  b 
  m =    y' 
 x' 
 b gibt an, um wieviele LE
 der Graph in y-Richtung
 verschoben ist.
Über das gelbe Steigungsdreieck kann man den Steigungsfaktor m berechnen. Es kann unterschiedlich groß sein, hat aber bei derselben linearen Funktion immer dasselbe Verhältnis zwischen den Werten y' und x'.
 m =   1   2   3   4   ...   Man nennt diese Koordinatenpaare 
 auch quotientengleiche Größenpaare.
 1,5   3   4,5   6   ... 
Die Verschiebungskonstante b lässt sich an der Stelle ablesen, an der der Graph die y-Achse schneidet  Sy(0/b).
Für diesen Punkt gilt immer x = 0.
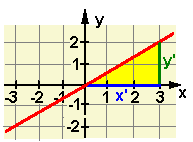
Die hier dargestellte Funktion hat die Funktionsgleichung    y =   2   x + 0   oder kürzer  y =   2   x 
 3   3 
Zum Zeichnen des Graphen einer linearen Funktion müssen bekannt sein ...
... entweder zwei Punkte des Graphen (am besten weit auseinander)
... oder ein Punkt auf dem Graphen und der Steigungsfaktor m für ein Steigungsdreieck.
Bei einem negativen Steigungsfaktor verläuft der Graph von links oben nach rechts unten.
Den Schnittpunkt des Graphen mit der x-Achse nennt man Nullstelle N(?/0) sein y-Wert ist immer 0.
Allgemeine Tipps:
Mit der Tabulatortaste gelangt man jeweils ins jeweils nächste Eingabefeld der Übungsaufgaben.
Leerzeichen werden als Fehler gewertet und 100% gibt es nur, wenn vor dem Prüfen alle Felder richtig ausgefüllt sind.
Seite druckenDiese Seite drucken  dwu-Logo © 2006 Schließen Fenster schließen